What is Linear Regression ?

Linear regression is a statistical approach used to model the relationship between a dependent variable and one or more independent variables by fitting a linear equation to observed data.

Linear Regression in Time Series

“Time” dimension in an analytical context is always forward looking and equally incremented. In this context, linear regression helps us understand how any independent variable is influenced against the dependent variable i.e. time period.

Assumptions in Linear Regression

  1. Linearity : The independent and dependent variables are related in a linear fashion. This suggests that changes in the dependent variable (s) are linearly followed by changes in the independent variable(s).
  2. Independence : The observations in the dataset are unrelated to one another. This signifies that the value of the dependent variable for one observation is independent of the value of the dependent variable for another.
  3. Normality: The errors in the model are normally distributed and the variance of error is constant
  4. No multicollinearity: There is no high correlation between the independent variables. This indicates that there is little or no correlation between the independent variables.

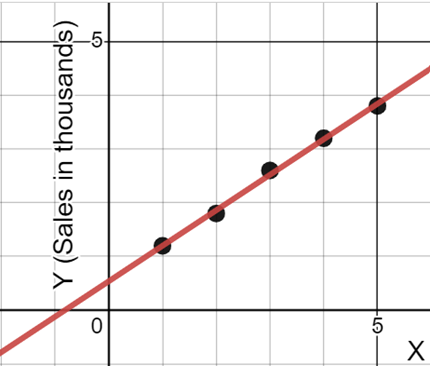
Example

Equation of Linear Regression

Y=a0+a1*X

X is the independent variable and it is plotted along the x-axis.

Y is the dependent variable and it is plotted along the y-axis

Values of a0 and a1 are calculated using the below formulae 

  • a1=((xy)`-x`y`) / (x2)`-x`2
  • a2= y` – a1 * x`

Let X stand for the week and Y stand for sales.

X(Week)

Y(Sales in thousands)
11.2
21.8
32.6
43.2
53.8

X

Y

x²

X*Y
11.211.2
21.843.6
32.697.8
43.216112.8
53.82519
SUM1512.65544.4
AVERAGEX`=3Y`=2.52(X2)`=11(XY)`=8.88

a1=0.66 , a0=0.54

Regression equation  : Y  = a0 +a1*X

Y = 0.54 + 0.66X

Dataset Information

The sample dataset from the Industry schema is as follows, with a focus on the “salesorderheader” relation.

Field

Type

Candidate Variable
OrderIDCharacter
CustomerIDInteger
ShipDateTimestamp✔
SalespersonemployeeIDInteger
ShipMethodIDInteger
TerritoryIDInteger
SubTotalNumeric✔

Number of records : 1561

Candidate keys

Number of unique values

Max Value

Min Value
Subtotal623129,261.2542.29
ShipDate6752014-05-012011-06-01

Workflow

Reading & Manipulation of data

  • The data is read via DB connector node and fed into KNIME via DB reader after choosing appropriate relation and extracting the necessary primary candidate key.
  • SubTotal values are grouped by applying an aggregate function sum, and this grouping is based on week, month and year.
  • Convert the time variable to incrementing integer to overcome tool restriction

Prediction

  • Execute the “Linear Regression Learner” node on the data present in the “SubTotal” column for the weekly and monthly data.
  • Add the number of prediction nodes for the prediction step. The granularity of source data is maintained here.
  • Execute the “Regression Predictor” node on the weekly and monthly data.

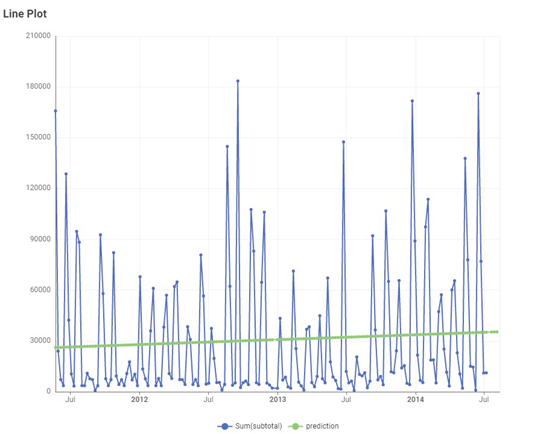
Visualization

Monthly data

Monthly data : green line → best fit line

Weekly data

Green line → best fit line

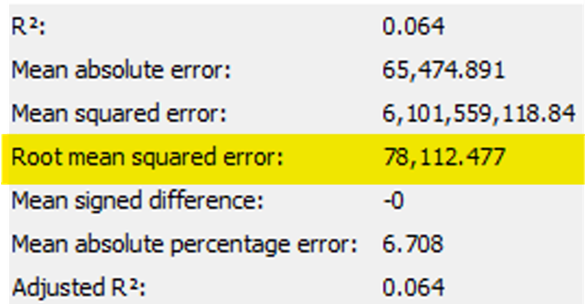
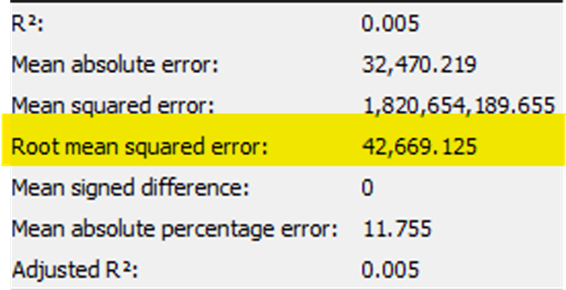
Forecast Accuracy

Monthly data

Weekly data

Conclusion

  • Linear regression is used to establish and quantify the relationship between a dependent variable and one or more independent variables.
  • Predicting and understanding the behavior of the dependent variable based on the values of the independent variables.
  • A Lower RMSE Value indicates best fit line
  • There is a higher RMSE value in monthly data suggests that the line is not best fit
  • Based on the two observations observations above it is imperative that wide variations in data points leads to poor accuracy
  • Eliminating outliers can improve accuracy but it should not impact the stability of data

Authors

  • VedhashreeU
  • Kaptain